Représentations graphiques

Problèmes

Proposer aux élèves une représentation graphique

 des différentes structures élémentaires qui seront utilisées dans les problèmes

 Cœur des problèmes

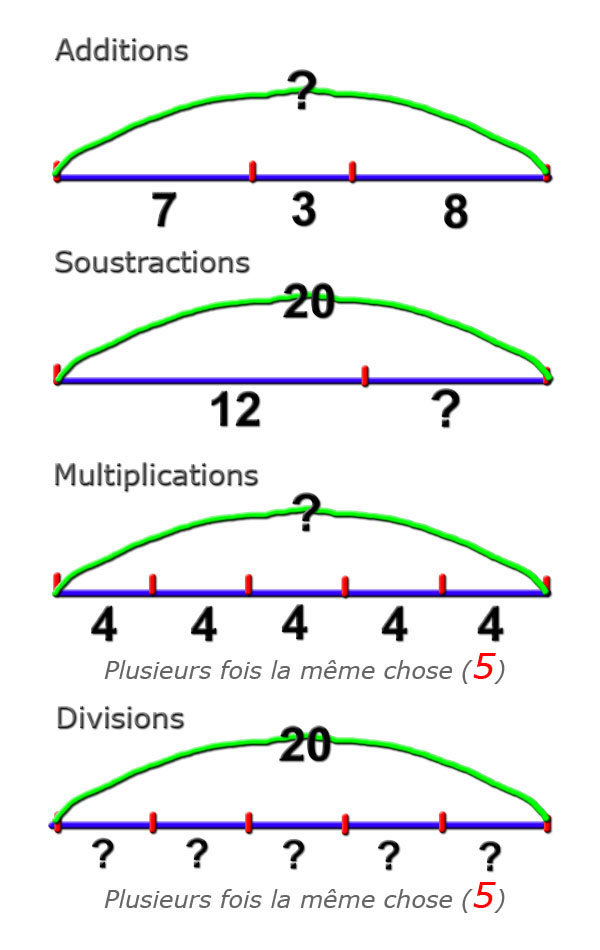
Il faut proposer aux élèves une représentation graphique des différentes structures élémentaires qui seront utilisées dans les problèmes.

Une fois les concepts numération/opérations bien acquis, on se sert de la représentation linéaire parce qu'elle est très lisible.

Ces structures élémentaires seront comprises et mémorisées au fur et à mesure du CE1.

- la place et le nombre de données

- le total ou sous-total (arc de cercle)

- la place du point d'interrogation

- l'expression "plusieurs fois la même chose et la donnée invisible" pour la multiplication et la division.

Ces structures élémentaires peuvent se retrouver imbriquées dans des problèmes plus complexes.

NB : la représentation 12 + ? = 20 pourra être remplacée par 20 - 12 = ? par la suite.

(La donnée invisible)

 Méthodologie

Au début du CE1, je donne à mes élèves des pages de catalogue (avec des photos d'objets et leur prix).

Ils doivent découper ce qu'ils veulent "acheter".

Au début, je leurs dis : 3 objets.

"Combien ça coûte en tout ?"

ou

"Combien vas-tu dépenser ?"

Ils se servent de la calculatrice.

Nb : on peut aborder les problèmes d'une façon différente. L'objectif, c'est d'arriver aux représentations graphiques.

Bien sûr, on étudie en même temps la monnaie (pièces et billets).

Les concepts "acheter" et "combien ça coûte" font partie de leur vie.

Ils collent sur la feuille les objets choisis puis ils écrivent la valeur de l'objet dans une étiquette.

Avec la calculatrice, ils trouvent combien ça coûte.

Pour obtenir la bonne réponse, ils doivent avoir la bonne méthodologie :

C (clear) 19 + 29 + 69 =

Ils s'entraident.

Nb : l'apprentissage de la calculatrice a été fait dès le CP.

 Structures élémentaires

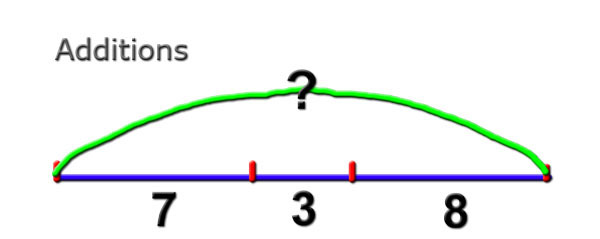
Additions

On étudie la représentation graphique "Additions" : les données, l'arc de cercle pour le résultat et le "?" pour la solution.

Notions maximum, minimum et entre

Avec l'achat de plusieurs objets ils doivent dépenser :

- au "maximum" 100 euros

- au "minimum" 100 euros

- "entre" 100 et 200 euros

Ils doivent tâtonner (calculatrice obligatoire).

Multiplications

La multiplication n'est pas compliquée à comprendre. Sa représentation graphique non plus.

4 x 5 = 4 + 4 + 4 + 4 + 4

Les élèves, au début du CE1, on tendance à utiliser l'addition avec leur calculatrice. C'est normal. C'est plus naturel. Plus tard, ils comprennent que pour faire 4 x 15 avec l'addition (calculatrice), cela devient fastidieux !

Dans la multiplication, ce qui est difficile, c'est la notion de donnée invisible. Dans la représentation à droite, il s'agit de la donnée "5"

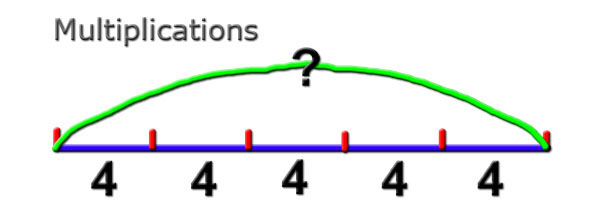
5 fois la même chose

(La donnée invisible)

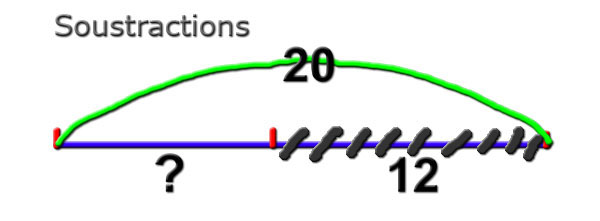
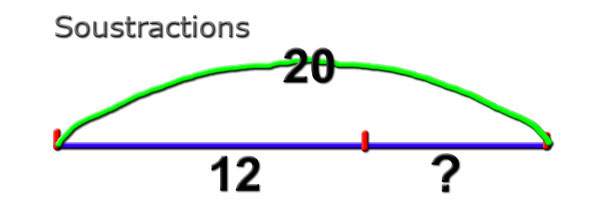
Soustractions

On aborde le reste avec le complément :

Ils ont 20 euros. Ils achètent un objet à 12 euros.

12 + ? = 20.

Plus tard, on va représenter la soustraction de cette manière :

20 - 12 = ?

La notion "enlever" est plus apparente comme cela.

Nb : ils ont l'habitude de barrer avec le dessin des soustractions.

Divisions

Au mois de mai, on abordera la division.

Partage et répartition.

Comme dans la multiplication, ce qui est difficile, c'est la notion de donnée invisible. Dans la représentation à droite, il s'agit de la donnée "5"

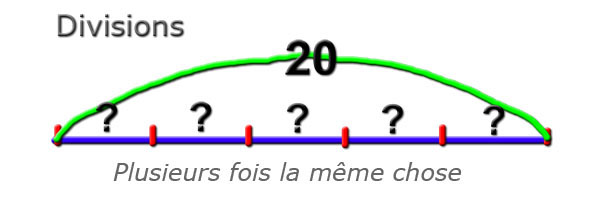
5 fois la même chose

(La donnée invisible)

 Structures complexes

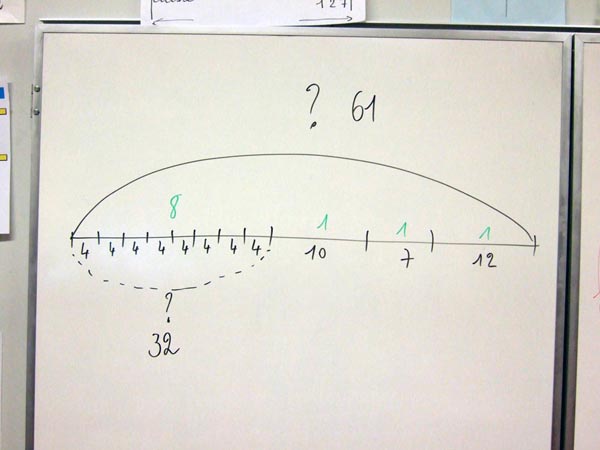
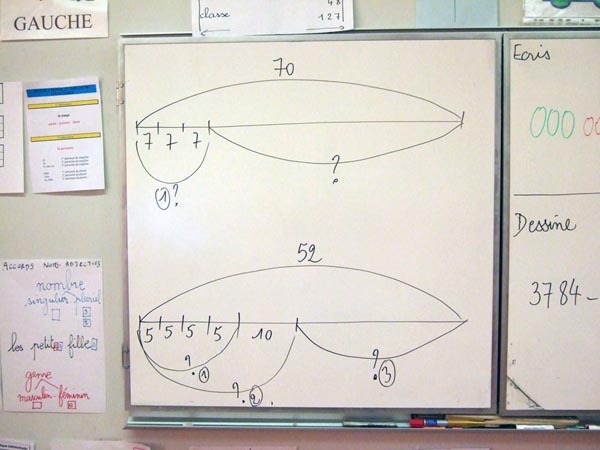
Quand les structures élémentaires sont bien comprises et bien mémorisées, on doit apprendre aux élèves à les retrouver dans des structures plus complexes.

- Un problème complexe peut se décomposer en tâches élémentaires,

- Il y a plusieurs étapes pour arriver à la solution finale (plusieurs points d'interrogations),

- Il y a une chronologie dans les étapes.

C'est un véritable apprentissage.

Le visuel permet de tout comprendre.

 Savoir-faire

A partir d'une représentation graphique, les élèves devront choisir le bon opérateur.

A partir d'une représentation graphique, les élèves devront écrire un problème.

A partir d'un problème, les élèves devront faire une représentation graphique.

En fin d'année, les élèves doivent savoir écrire l'histoire (problème), l'opération en ligne, l'opération en colonne et la réponse.

 Conclusion

Les représentations graphiques qui expliquent les concepts fondamentaux doivent être au cœur des apprentissages.

Un problème avec des mots, c'est beaucoup trop abstrait pour que les élèves en difficulté comprennent.

Les élèves sont plein de bonne volonté. Mais, souvent, s'ils ne produisent rien c'est qu'ils ne savent même pas ce qu'on leur demande !

La représentation graphique est le support incontournable des apprentissages.

L'école : le lieu où on explique les choses !

Daniel CLERC

 Photos math CE1