|
|
|
|
Les élèves apprennent
à lire et à compter à l’école...
... mais apprendre en
comprenant, c'est essentiel !
Les représentations
graphiques sont indispensables pour la compréhension :
elles offrent le concret.
Les concepts fondamentaux du
lire/écrire et compter doivent donc avoir leurs représentations.
Les élèves les plus forts
s’approprient très vite le savoir. Les élèves en difficulté y feront tout
le temps référence.
Les élèves qui ont compris
sont heureux ! Ils deviennent responsables et autonomes. Ils peuvent
enseigner aux plus faibles.
Le présent
Quand on analyse les
instructions officielles et les manuels
de lecture et de math du cycle 2 sous l’angle des représentations
graphiques, on s’aperçoit vite des progrès qui restent à faire.
Cette absence de
représentations graphiques est révélatrice des lacunes au niveau du
comprendre.
L’Avenir
Les représentations
graphiques des concepts fondamentaux existent !
C’est l’objet de mon site !
En mettant au centre de
l’enseignement ces concepts associés aux représentations graphiques, on
permettra aux élèves de mieux comprendre.
Le changement doit venir de
l'évolution des programmes officiels et de la formation des maîtres.
Mais chaque enseignant doit
se poser cette question : « Quelles représentations graphiques sont
utilisées dans ma classe pour faire comprendre aux élèves les concepts
fondamentaux ? »
Daniel Clerc |
 
 
Lire/écrire
& numération/opérations imbriqués
|
|
Le lire et l'écrire sont totalement
imbriqués.
Et bien pour la numération et les
opérations, c'est la même chose.
L'un sert à l'apprentissage de l'autre.
Voilà ce que les représentations graphiques
permettent de faire comprendre.
|
 
|
|
|
J'ai envie de faire le parallèle avec l'émission célèbre 'C'est
pas SORCIER'
pour faire comprendre ma démarche pour l'enseignement du lire/écrire et du
compter.
Explications scientifiques avec support graphique pour bien comprendre.
|
 
|
|
|
Non, désolé ! Pas de miracle...
Mais apprendre en comprenant, c'est essentiel !
Les plus forts apprennent encore plus vite.
Les plus faibles savent ce qu'ils ont à
apprendre et à comprendre. Les choses sont claires !
Pour apprendre, il faut être serein.
Les problèmes psychologiques,
le problème des non-apprenants, c'est autre
chose...
|
 
|
|
|
Ce que je propose pour la lecture n'est pas une méthode !
Les concepts qui sont liés à l’apprentissage
de la lecture sont abstraits…
Pour que les enfants (et les adultes...)
comprennent ces concepts, il faut « forcément » passer par les
représentations graphiques...
Et c’est ça qui est nouveau !
|
 
|
|
|
- j’apporte des solutions nouvelles à l’enseignement.
Florian (15 ans) : - j’ai appris à lire !
Nul n’est prophète en son pays !
Dans cette lettre, je vais essayer de t’expliquer ma vision
des choses.
Je vais transposer avec le vélo.
Dans ma classe, il y a 12 CP et 10 CE1 que je garde 2 ans.
Ce jour là, il y avait 2 absents. J'avais 3 CE2 en plus (maîtresse absente).
J’ai demandé aux élèves de dessiner un vélo. Pas de
conseil. Pas de modèle sous les yeux.

Le dessin des CP

Le dessin des CE1

Tous les élèves savent, dans l'ensemble, faire un peu du vélo.
En observant les dessins, tu peux constater que les vélos
des CE1 sont plus élaborés que ceux des CP.
- les 2 points d’appuis : guidon, selle sont dessinés
- les pédales : 6 CP
- les rayons : c’est remarquable !
- le cadre : il est, la plupart du temps, attaché aux
pneus chez les CP mais également chez certains CE1
- la chaîne : 4 CP sur 11
Le dessin des CE2

Les enfants ont appris à faire du vélo. Leur cerveau a bien
travaillé !
Mais quand on leur demande de dessiner, on s'aperçoit
qu'ils ont besoin de l'école pour mieux comprendre les choses.
Florian, tu me dis que tu as appris à lire. C'est vrai !
Ton cerveau a su mémoriser les mots.
Le rôle de
l'école, c'est de bien expliquer les mécanismes du lire/écrire et de la
numération/opérations/problèmes en
se servant de solutions graphiques car sinon les concepts sont trop abstraits
pour les élèves.
Daniel (père)
|
 
|
|
|
Je vais transposer avec le vélo :
L'acte "faire du vélo" :
Sur un vélo, l'enfant monopolise ses capacités
(intellectuelles et physiques) pour avancer et ne pas tomber.
Mais une fois à l'arrêt, donc en dehors de
l'acte "faire du vélo", l'enfant est capable d'apprendre et de
comprendre les concepts
direction/équilibre/gravité ; transmission/roue/engrenage/chaîne ;
sécurité/frein...
Une fois ces concepts acquis il sera plus
autonome et plus responsable : il sera capable de prendre des décisions. Il
pourra aider/expliquer à ceux qui ont plus de difficultés.
L'acte "lire" :
L'enfant monopolise ses capacités
intellectuelles pour comprendre le sens et apprécier un texte.
Mais une fois le texte "lu", donc en dehors de
l'acte "lire", l'enfant est capable d'apprendre et de comprendre tous les
mécanismes de la lecture.
|
 
|
|
|
Un parent d'élève était dans ma
classe pour parler de son enfant.
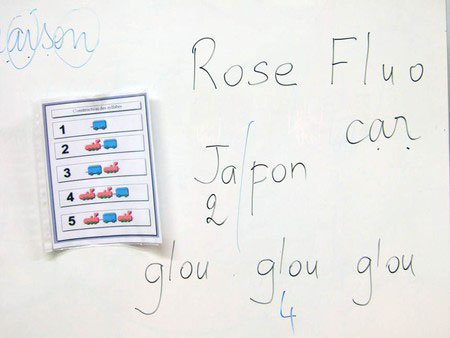
Je lui avais expliqué les constructions
des syllabes numérotées de 1 à 5.
|
Je me suis permis de lui demander de me dire le numéro
de la syllabe 'pon' dans le mot 'japon'
Il m'a répondu
5.
J'ai demandé à son fils de me dire le
numéro.
Il m'a répondu
2.
Le parent avait vu
'p', 'o', 'n'
: consonne + voyelle + consonne (comme la majorité des français !)
L'enfant avait vu
'p', 'on'
: consonne + voyelle (comme tous mes élèves !)
Et pour lire "pon", il faut une
consonne (p) et une voyelle (on).
|
|
|
|
|
Le parent raisonnait au niveau
des lettres de l'alphabet. |
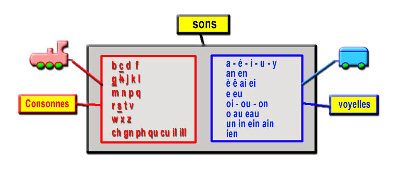
L'élève raisonnait au niveau des sons. |
 
|
|
|
La représentation des mots ne donne aucune
explication

|
|
|
|
Avec les représentations
graphiques
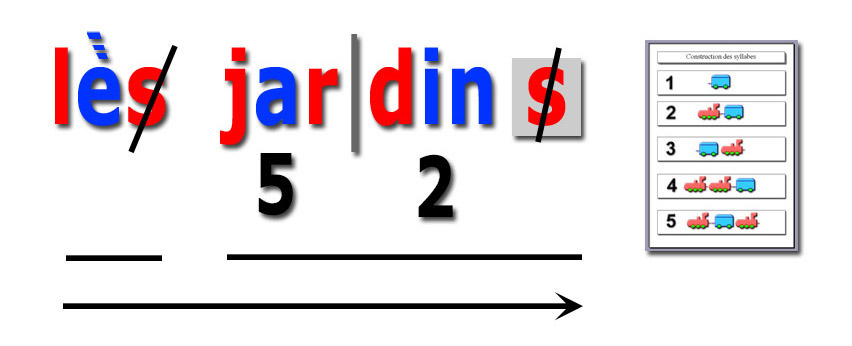
Cette représentation des mots explique et
visualise :
- le sens de la lecture,
- le nombre de mots,
- la notion de voyelles/consonnes,
- la notion de
graphèmes/phonèmes,
- les syllabes,
- la construction des syllabes,
- les accents disparus (lès),
- la case des accords,
- les lettres muettes.
Lire - Ecrire avec les représentations
graphiques
|
|
|
Les représentations des
nombres et des opérations ne donnent aucune explication

Pourquoi, après le nombre 9, on écrit dix
avec le chiffre 1 et le chiffre 0 (10) ?
Pourquoi, après le nombre 9, on n'écrit pas
dix avec le chiffre 0 et le chiffre 1 (01)?
Pourquoi 10 (une dizaine et zéro unité) ne se
dit pas dix zéro ?
Pourquoi le nombre 584 (centaines, dizaines,
unités) ne s'écrit pas 485 (unités, dizaines, centaines) ?
Les signes "+",
"-",
"x"
n'expliquent rien.
Le chiffre de la retenue n'explique rien.
Pourquoi 100 = 1 ?
Numération & opérations avec les
représentations graphiques Problèmes
|
 
 
|
|
|
Le point
central de l'enseignement doit être les représentations graphiques
(visuel/concret) qui expliquent les concepts fondamentaux.
Ces représentations graphiques doivent être
affichées à chaque séance.
Les élèves les
plus forts comprennent très vite et s'approprient le savoir.
Les plus
faibles y feront référence toute l'année.
Une fois qu'il a compris, l'élève peut être
acteur de ses apprentissages.
Elève "enseigné" / élève
"enseignant"
  |
 
|
|
|
La pédagogie linéaire, c'est le trait bleu. On avance
régulièrement. Ce n'est pas une pédagogie satisfaisante.
La pédagogie que j'utilise, c'est une pédagogie avec des
allers-retours, qui parfois, si le besoin s'en fait sentir, me fait revenir au
début pour récupérer les enfants en difficulté. Elle fait parfois des grands
bonds (pointillés) pour alimenter les enfants très doués.
Cette pédagogie avance au rythme des acquisitions des élèves et par conséquent varie en fonction des
classes. Comme les enfants sont très actifs, on les voit faire et on vérifie
continuellement leur progression.
|

|
 
Représentations graphiques
|
|
Le 1° apprentissage, c'est la notion
de catégorie !
Les
enfants qui arrivent de la Maternelle raisonnent, bien souvent, à un seul
niveau.
Pour
eux, pigeon – canard – oiseau – poule sont 4 mots qui signifient quelque
chose mais il n’y a pas de niveau hiérarchique.
Faire comprendre la notion de catégorie peut
se faire de différentes manières :
- On peut expliquer : il y a des
choses qu'on peut regrouper. On met dans une étiquette le mot qui désigne toutes
ces choses.
- On peut donner des exemples : le
chêne, le bouleau, le platane sont des arbres.
- On peut poser des questions : Dites moi des noms de planètes !
- On
doit faire une représentation
graphique avec les étiquettes !
Les élèves du cycle 2 ont besoin de
travailler dans le concret pour comprendre.
Si vous n'aviez pas compris mes
explications ci-contre, le graphique vous éclaire !
Premier apprentissage
|
 
Représentations graphiques
|
|
Ils sont affichés au tableau
à chaque séance.
|
 |
 
Représentations graphiques
Le lire/écrire sont
totalement imbriqués.
|
|
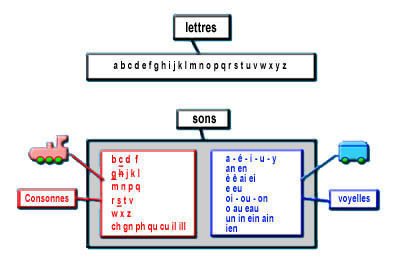
Représentations graphiques
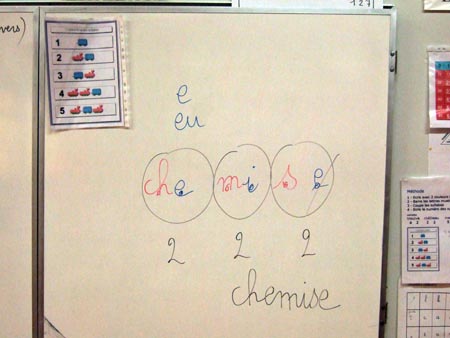
Lire
La représentation graphique pour la
construction des syllabes à partir des concepts voyelles/consonnes ;
graphèmes/phonèmes n'existe pas à l'école à l'heure actuelle (sauf dans ma
classe).
Ce n'est pas moi qui ai eu l'idée
des
wagons et des locomotives mais je n'ai jamais trouvé
mieux !
Les locomotives, ce sont les consonnes. Les
wagons, ce sont les voyelles. Le train, c’est la syllabe.
Il y a
l'idée d'accrochage, comme dans la
combinatoire.
Grâce à la représentation graphique sous
forme de trains, on peut donner des numéros à chaque construction de syllabes.
On travaille d'une
manière scientifique.
|
 |
|
train numéro 1
1 voyelle
1 wagon
exemple : a
en |
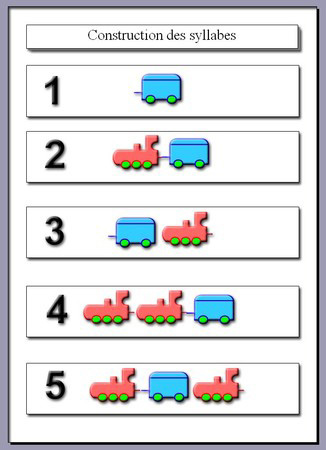 |
|
train numéro 2
1 consonne +
1 voyelle
1 locomotive +
1 wagon
exemple : ra chou
vain |
|
train numéro 3
1 voyelle +
1 consonne
1 wagon +
1 locomotive
exemple : al
il es |
|
train numéro 4
1 consonne +
1 consonne + 1 voyelle
1 locomotive +
1 locomotive + 1
wagon
exemple : tro blan phra |
|
train numéro 5
1 consonne +
1 voyelle + 1 consonne
1 locomotive +
1 wagon + 1
locomotive
exemple : tar
bir
sour |
|

La locomotive à vapeur et les wagons, c'est une
représentation universelle du train. |
 |
|
Représentation graphique
accent pointillé
Où faut-il mettre les accents ?
electricite
Nous savons parce que nous avons mémorisé le mot :
électricité
Les enfants du CP, logiquement, ont envie d'écrire :
élèctricité
On doit leur apprendre cette règle :
|
Dans la syllabe, le "é" et le "è" perdent leur accent quand ils sont suivis
d'une consonne. |
Et pour que cela soit bien clair, il faut introduire la représentation graphique
: accent pointillé

La consonne, c'est 1, 2 ou 3 lettres !
Exemple : bec,
soleil,
abeille !

Un exemple !
|
|
Comme pour la numération,
Représentation graphique
lettre barrée

Dans le mot
'Christian',
c'est le 'h' qui ne se
prononce pas. On lit bien 'cristian'.
Dans le mot 'chat',
le 'h' du 'ch'
fait partie de la consonne (graphème/phonème).
Le 't' ne se
prononce pas. 'cha'. On doit
barrer le 't'.
(Le t peut se retrouver par
un mot de la même famille - chaton).
C'est un véritable apprentissage qui permet d'éclaircir
la lecture et l'orthographe.
Il y a des lettres qu'on ne prononce pas. Mais elles
existent.
La représentation graphique :
lettre barrée permet de voir si
l'enfant a compris.
Au début du CP, c'est l'enseignant qui le fait tout le
temps au tableau.
Puis, naturellement, c'est l'élève qui va devoir le
faire sur les mots travaillés en classe. Au CE1 (puis au cycle 3) les enfants
devront le faire sur n'importe quel texte (relativement court).

Un exemple !
|
|
Comme pour la numération,
Représentation graphique
trait = mot

Les enfants doivent
tracer des traits (représentation graphique).
Ces traits doivent correspondre au nombre de mots qu'ils perçoivent
à l'écoute d'une phrase orale.
|
 
Représentations graphiques
Le lire/écrire sont
totalement imbriqués.
|
|
Un mot est constitué de syllabe(s)
Les syllabes, ce sont des sons
fabriqués dans la bouche (consonnes) et dans la gorge (voyelles)
Ce qu’on dit c’est le phonème, ce
qu’on écrit c’est le graphème.
Il faut apprendre aux élèves les
constructions des syllabes :
«
Trou » et «
cla »
c’est la même construction (2 consonnes et
1 voyelle)
«
si » et «
phan » c’est la même construction (1
consonne et 1 voyelle)
Pour que les enfants comprennent
ces notions, il faut utiliser les couleurs, une représentation
graphique et un numérotage des constructions.
|
|
Ecrire à partir de
mots copiés
 |
 |
|
Ecrire des syllabes
Les élèves
devaient écrire la syllabe numéro 5 (consonne - voyelle -
consonne) avec 4 lettres.
J'ai écrit au tableau les réponses des élèves
(ardoise).
|
 |
|
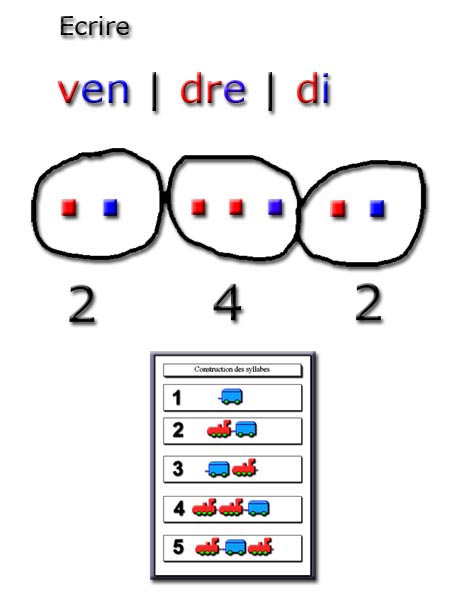
Ecrire
à partir de mots dictés
Méthode :
1) Compter le nombre de syllabes : les élèves
tracent les ronds.
2) Ecrire, sous chaque rond, le
bon numéro : les élèves sont obligés de réfléchir (avant d'écrire) à la
construction de la syllabe.
3) Mettre au tableau, dans les ronds, les points avec des couleurs.
L'élève sait combien il y aura de locomotives
(consonnes) et de wagons (voyelles). Il connait également l'ordre de
cette construction.
Il a
toutes les informations pour réussir à écrire ses syllabes et par
conséquent son mot.
4) Ecrire les voyelles et les consonnes.
5) Correction collective : un élève, au tableau, écrit la réponse
ou un élève me dicte les lettres
ou un élève me dicte les sons.
6) Le mot est écrit en entier (sur la feuille
et au tableau) et on 'prend' la
photo.
Tous les jours. Trois mots par jour.
|
 |
|
Représentation graphique
cases
des accords

il faut
faire apparaître les accords avec des cases colorées
rouge pour
le genre -
bleu pour le nombre

Pour le verbe, c'est une grande case
(radical/terminaison)
|
 
Représentation graphique
|
|
Le 'petit chien', c'est très ancien.
L'élève a une représentation graphique de
chaque élément qui constitue la plupart des lettres.
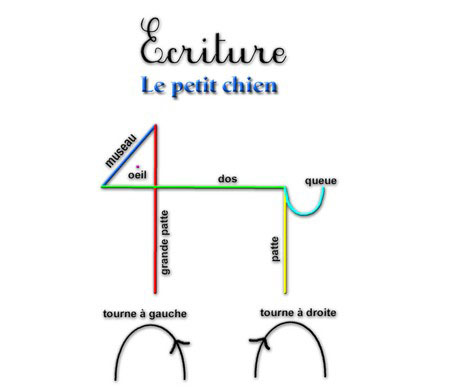
Ecriture |
 
Représentations graphiques
La numération et les
opérations sont imbriqués.
|
|
Représentations graphiques
Numération
Pourquoi 10, après 9, s’écrit avec un
« un » et un « zéro » ?
Pourquoi 100 = 1 ?
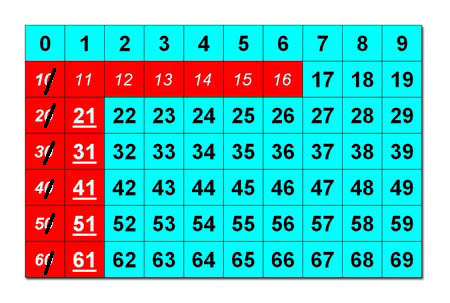
La représentation linéaire de la
suite des nombres (indispensable par la suite) n'explique en rien la numération :

En dessinant les croix (unités) et les
paquets (dizaines, centaines, mille) de différentes couleurs, les choses
sont concrètes.
La numération avec les différents niveaux
des paquets permet également la compréhension des puissances.
L'extra-terrestre (ou le robot) donne le nombre de doigts
: c'est la règle du fonctionnement.
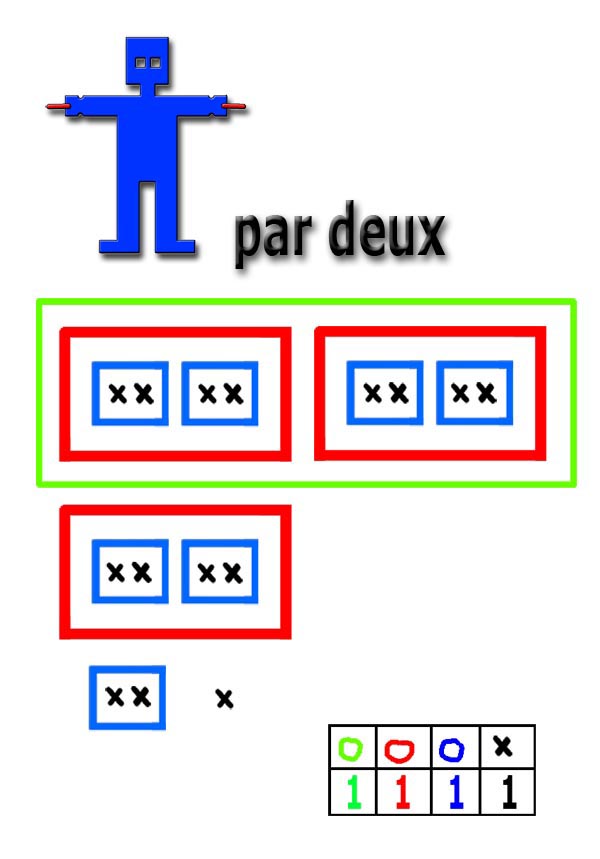  
Avec ces représentations graphiques
(extra-terrestre, paquets, croix, traits, couleurs), l'élève
comprend la relation entre le nombre dessiné, les chiffres et
les mots.
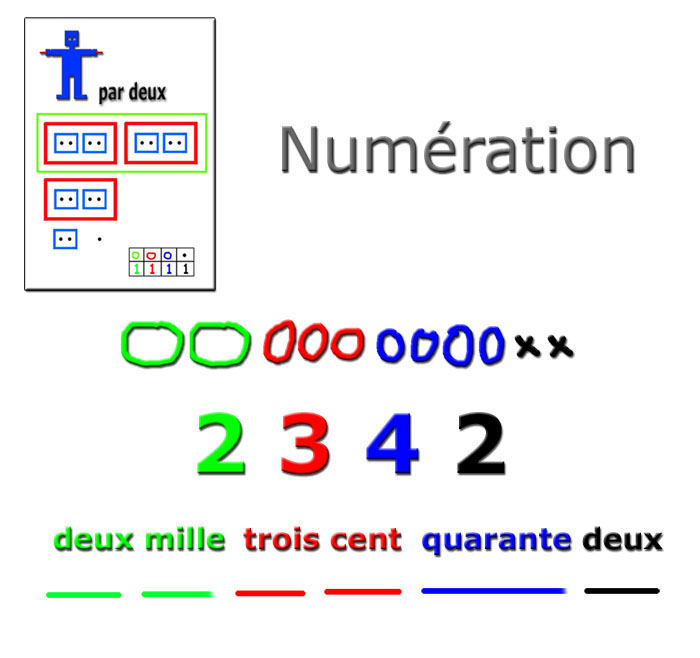 
La représentation graphique des paquets et
des croix permet de tout expliquer :
avant-après, moitié-double, complément à 10,
chiffres muets, zéros, la position, le 70-80-90
|
|
Comme pour la lecture,
Représentation graphique
chiffre barré
permet d'éclaircir la compréhension. Il y a des chiffres qu'on ne prononce
pas.
 |
|
Comme pour la lecture,
Représentation graphique
trait
= mot
permet d'expliquer certaines difficultés visuellement.
 |
|

Quand les élèves sont à l'aise pour naviguer entre
- le dessin des paquets et des croix,
- l'écriture en chiffres et l'écriture en lettres,
on peut dire qu'ils ont compris la numération.
|
 
Représentations graphiques
Sens des opérations
La numération et les
opérations sont imbriqués.
|
|
On se sert de l'apprentissage de la
numération pour expliquer le sens des opérations
Additions
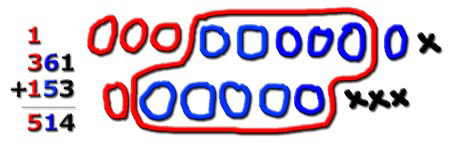
On ajoute.
Dix paquets bleus -> un paquet rouge
La retenue est évidente !
|
|
Multiplications
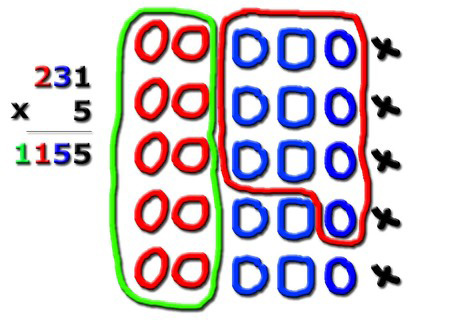
On ajoute plusieurs fois la même chose.
Les retenues sont évidentes !
|
|
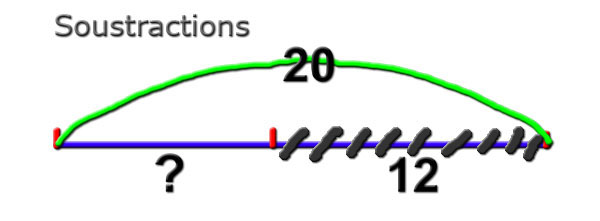
Soustractions

On enlève.
|
|
Soustractions à retenue

Les manipulations mettent en évidence la
compréhension.
Quand les élèves sont capables de
'dessiner' les opérations et qu'ils se rendent compte que le calcul (ou la
calculatrice) donne le même résultat, on peut dire qu'à ce moment là, tout le
monde est heureux : l'enseignant et l'enseigné !
|
 
Représentations graphiques
|
|
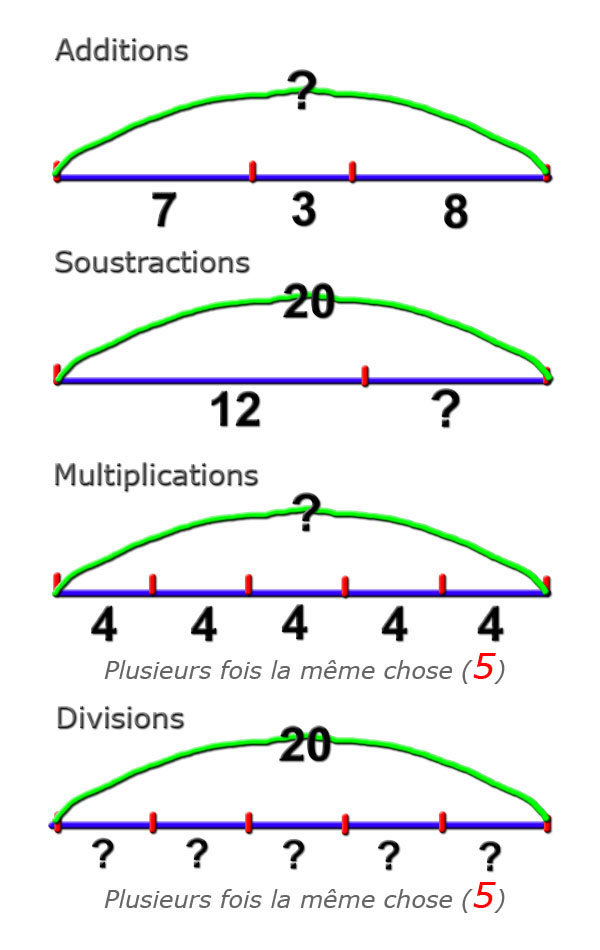
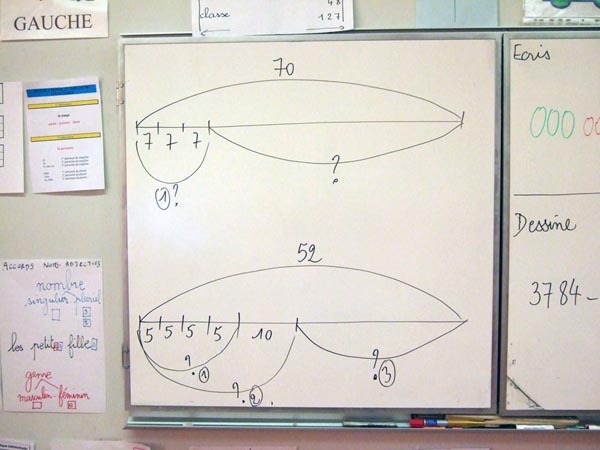
Il faut proposer aux élèves une représentation
graphique des différentes structures élémentaires qui seront
utilisées dans les problèmes.
On se sert de la représentation linéaire parce
qu'elle est très lisible.
Ces structures élémentaires seront comprises et
mémorisées au fur et à mesure du CE1.
- la place et le nombre de données
- le total (arc de cercle)
- la place du point d'interrogation
- l'expression "plusieurs fois la même chose"
et la donnée "invisible"
pour la multiplication et la division.
Ces structures élémentaires peuvent se
retrouver imbriquées dans des problèmes plus complexes.
C'est un véritable
apprentissage.
|
|

|
|
 
|
|
|
L'espace, le temps, le résumé, l'observation
ont besoin pour être compris de solutions concrètes.
Fondamentaux
Multimédia
|
 
|
|
|
Au début de l'année, quand je demande à mes CE1 de faire lire
les CP débutants tous les jours en fin de journée, il se passe quelque chose
d'important dans la psychologie des élèves.
Ils changent de statut.
Ils doivent utiliser leurs savoirs et
savoir-faire (encore hésitant) pour les autres.
Ils trouvent alors une profonde motivation à
s'améliorer eux-mêmes pour être à la "hauteur" vis à vis de leur
tâche.
Un peu plus tard, quand ils doivent aider les
CP à découper les mots, ils n'ont pas droit à l'erreur.
Mais cela fonctionne bien car les élèves du
CE1 ont parfaitement compris les mécanismes grâce aux représentations
graphiques. |
 |
|
Quand ils doivent apprendre aux CP comment utiliser le compas ou
comment utiliser le dictionnaire, c'est plus difficile.
Les CE1 ont les compétences. Mais, au
moment d'expliquer aux CP, certains ne savaient pas trop quoi dire ou par 'quel
bout commencer' !
J'ai repris les CE1 avec moi un peu plus
tard et on a revu ensemble ce qui était important. Les CE1 étaient très
attentifs car ils avaient besoin de ces informations pour pouvoir 'bien
enseigner'.
Pédagogiquement, c'est vraiment là où c'est
passionnant !
|
 |
|
Si on veut que l'apprentissage soit
complet, il faut que les élèves deviennent à certains moments
des élèves "enseignants".
C'est très enrichissant pour tout le monde : adultes et enfants.
Un enfant qui a compris peut expliquer (avec le
support des représentations graphiques) à ses camarades en difficulté dans tous
les niveaux de classe.
Les élèves doivent être acteurs de leurs
apprentissages. |
 |
|
Nb : il n'y a rien de figé.
Ce n'est pas forcément CE1 ou CP.
Les CP les plus doués deviennent rapidement
élèves "enseignants" et les CE1 en difficulté vont continuer à être
"enseignés" dans les domaines où ils ont besoin de soutien. |
|
Les CM
et la liaison avec la maternelle |
 
Continuité dans les apprentissages
|
|
Le comprendre, avec support des solutions
graphiques, ne doit pas être enseigné qu'au Cycle 2.
Nous savons tous que les acquis chez
les enfants en difficulté sont fragiles.
Ces élèves ont besoin de repères stables.
Il faut donc que tous les fondamentaux
soient présents au cycle 3 : affichages, enseignement, documents,
soutien par les élèves qui ont compris.
|
 
|
|
|
Un enfant doit écrire la syllabe "lac"
Il écrit "la"
L'enseignant va lui dire : tu t'es trompé.
Il va répéter la syllabe "lac",
plusieurs fois. En insistant sur le phonème "c"
Il peut dire les lettres "l",
"a",
"c"
Il peut dire : il manque un "c"
Il peut indiquer avec le doigt l'endroit où
il manque la lettre.
Il peut décomposer la syllabe en une
séquence de phonèmes : "l",
"a",
"c"
C'est abstrait.
Avec le support des représentations
graphiques :

L'enseignant ou l'élève enseignant va
expliquer avec
le support des trains :
Tu as écris
le train 2
et il fallait fabriquer le
train 5.
Il manque une
locomotive à la fin.
C'est le "c"
(phonème) de sac
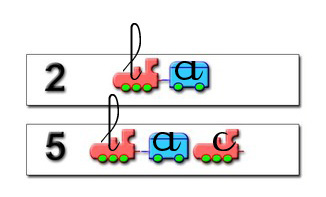

C'est concret.
|
L'enseignant aborde la retenue :

Je vous laisse trouver les explications...
C'est abstrait.
Avec l'apprentissage de la numération,
la retenue, ce
sont les élèves qui la découvrent !
Tout marche par dix. Quand il y a dix croix, on les
entoure.
C'est concret.
|
 
L'école doit offrir aux élèves un
enseignement global, scientifique et cohérent.
|
|
La transmission des connaissances pour les élèves dont le
cerveau a été traumatisé par les conditions de vie ou le cerveau
altéré par des troubles du développement n'est pas la priorité.
Et pourtant, dans la classe, ce sont ces élèves qui préoccupent
le plus et ils sont de plus en plus nombreux dans notre société.
Mais cela ne doit pas empêcher l'école d'évoluer
pour ceux qui sont en mesure d'apprendre.
Introduire la composante "compréhension" est essentiel.
Les enseignants disent souvent : - tu n'as pas appris ta leçon.
Les élèves, dans ces cas là, ne semblent pas traumatisés. Ils
n'ont pas fait l'effort de mémoriser.
L'expression des élèves en difficulté : - je n'ai pas compris.
Et là, il y a de la souffrance.
Sur mon site, mon objectif a été de décrire ce qui manque
actuellement dans l'enseignement : les représentations
graphiques qui expliquent les concepts fondamentaux doivent être
au cœur des apprentissages. Il faut également que les élèves
deviennent acteurs de leurs apprentissages : il ne faut pas
qu'ils soient seulement "enseignés" mais une fois qu'ils ont
compris, ils doivent être, à certains moments, "enseignants".
Je suis convaincu que lorsque les idées sont bonnes, elles
finissent par s'imposer. Surtout à notre époque où la
communication va très vite. Lorsque je propose à mes élèves (qui
ont un regard neuf) des choses fondamentales et qu'ils me disent
qu'ils ont compris, je sais que je suis dans le vrai car c'est
eux l'avenir !
Daniel CLERC
(18/12/2016)
Editeurs ? Mon livre avait été refusé par tous les éditeurs.
|
|